Introduction to Integers and Operations

Developing a basic understanding of number sense when studying integers is imperative. Building a solid definition of what an integer is provides a good start:

• An integer is a whole number
• It is not a fraction
• It can be either positive or negative
• All integers, positive and negative, have absolute values

Absolute Value and Integers

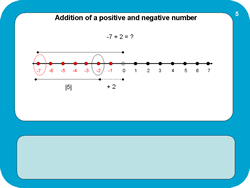
The absolute value of an integer is its numerical value regardless of its sign. For example, the integers -7 and 7 both have the absolute value of 7 which is noted as |7|. In regards to a number line the absolute value of a number is the distance between that number and zero. The numberline provides a helpful tool for explaining absolute value to students.

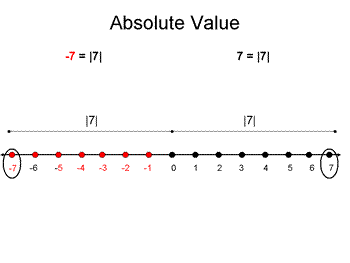
Students should also be able to find the absolute value between two integers regardless of their signs.

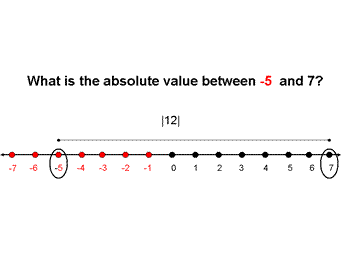
If a student knows the absolute values of numbers they can apply this knowledge to solving integer problems involving positive and negative numbers. You can view some examples of this in the slideshows below. Click on the link or image to view the slideshow. Note, the slideshow will open in a different browser window. If you are having problems viewing the slideshow, try installing the latest version of Adobe Flash Player.

Understanding operations or how to operate or use integers is an important concept in Algebra. It's important to review the basic rule of operating with integers. Here is a summary of the rules:

Rules of addition Sum of + #s is positive Sum of - #s is negative Sum of negative and positive number is difference of the two numbers, and the sign is the number with the greatest absolute value. Rules of subtraction Never subtract – add the opposite number (Define: opposite number). Ex. 3- (-2) is just 3 + (+2)=5 Rules of multiplication/division Multiplication and division of positive numbers are positive Multiplication and division of two negatives number is positive Multiplication and division of a negative and a positive are always negative

When solving a multi-step/ multivariable equation, students must understand how to use operations correctly. If they don’t have a solid understanding of the working of integers, they can’t do the problems or even identify where mistakes occur. Some of the most common mistakes made by beginning Algebra students include using operations incorrectly to solve equations.

For many students making mistakes with integers is normal. It may be helpful for them to analyze situations where mistakes occur and then systematically and methodically explain these mistakes and how to correct them.