Factoring a Quadratic

Key Information Topic B:

• Using Factoring
• First Step - Multiplying Binomials
• Factoring a Quadratic

Take some time to practice factoring a quadratic. Take the example of the quadratic below.

x² + 6x + 8

(ax² + bx + c)

Factor the above trinomial into two binomials by using the following steps.

1. Look at the third term, look at the factors of 8. (1x8, 2x4)
2. Which set of factors has the sum of b? 2 and 4
3. Look at the first term and factor it is (x * x) if so both binomials will start with x
4. In one binomial, we will add 2 and in the other we will add 4. Therefore, we will have (x+2)(x+4)

 

Notice that all terms are positive

If the terms look like this (x² - 6x + 8)
Then the binomials are (x-2)(x-4)

If the terms look like this (x² -2x - 8),
Then the binomials are  (x+2)(x-4)

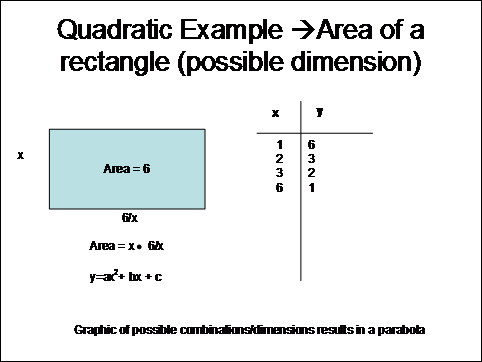
Application Example - Area of a Rectangle

Recall the example in Module 7 of finding the areas of a rectangle. This example provides an illustration of how a simple quadratic can be used to solve an  area problem.

If you were to graph the possible dimensions as ordered pairs, you would end up with a parabola.

The following slide illustrates how you can determine the quadratic equation of this problem from the data in the table.