Graphing and Understanding Quadratics

Topic A Key Information:

• Properties of Quadratics
• Graphing and Understanding Quadratics

 

As part of the introduction to quadratic equations, students need to graph the values from a simple quadratic. Students may find it helpful to complete this exercise with the help of a graphing calculator or graphing software. After graphing, students should discuss the results of what they see.

In the following example you will look at role of elements a,b,c in a quadratic equation, y=ax² + bx +c.

Breaking down the elements of the equation:

• y is the y coordinate from an ordered pair (x, y)
• x is the x coordinate from an ordered pair (x, y)
• a is the element with the power of 2
• b is the element with the power of 1
• c is the y intercept

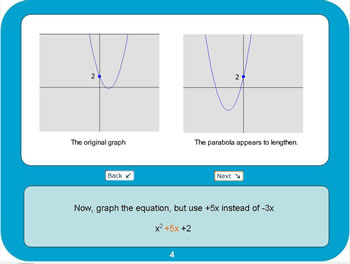
Using the expression, x²-3x+2, graph changes in the differences.

• Graph x²-3x+2.  Describe what you see.
• Replace +3x with -3x
• Use 5x instead of -3x (the graph will result in a non-solution because the line will not cross the x-axis).
• Use +5 instead of  +2
• 2x² is replaces x²
• Next, define what happens when the coefficient of x or x2 has a negative and or positive value.

View the slide show to see these changes graphed.

Click on the image to view the slide show in a new browser window

View a printable version of the slideshow content

Therefore, after completing the above exploration you can see that the following rules apply to quadratic function f(x)=ax² + bx +c:

• The positive/negative value of a determines whether the parabola faces up or down.
• The value of a determines the parabola’s width.
• The positive/negative value of b determines the horizontal position of the parabola.
• The value of b determines the parabola’s length.
• The value of c determines where the y intercept lies.

It is crucial that middle school students develop an understanding of these rules. Understanding and being able to explain the changes in variables helps students grasp the abstract concepts of changes in quadratic equations.

Idea for Classroom Application: Matching Graphs and Equations Develop a number of different graphs of both quadratic and linear equations.  Place these graphs on a worksheet. On a separate worksheet, include the original equations with a number of random equations added.   Have your students practice mapping the graphs with the equations.